Packing

Packing problems on graphs deal with the question of how to identify as many disjoint sub-structures of a given type as possible in a given graph. For example, we could try to find as many pairwise non-connected vertices as possible (maximum independent set) or as many disjoint cliques as possible (clique packing problem).

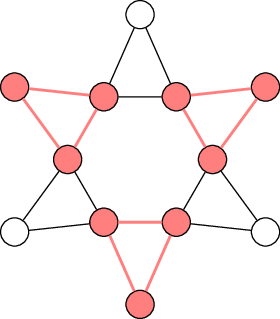
Example of clique packing for 3-cliques (aka triangles).

Independent set

An independet set in the vertex set of a graph is a subset of the vertices in which no pair of vertices is connected by an edge.

create_model	Create an ILP for the maximum independet set problem
extract_solution	Get a list of vertices comprising a maximum independent set

Clique packing

A clique is a fully connected subgraph. The clique packing problem asks for the maximal number of vertex disjoint cliques that can be found in a graph.

create_model	Create an ILP for the clique packing problem
extract_solution	Get a dictionary of vertex to clique assignments

Set packing

The set packing problem is asking for a maximum weight, disjoint sub-collection of the sets in a set system.

create_model	Create an ILP for the weighted set packing problem
extract_solution	Get a list of sets comprising a set packing

Heuristics

The methods in this section provide approximate solutions to the set packing problem constituting admissible solutions from which to start the exact optimisation.

get_heuristic

Greedy heuristic for the set packing problem

Details

graphilp.packing.max_indset.create_model(G)

Create an ILP for the maximum independet set problem

Parameters

G – an ILPGraph

Returns

a gurobipy model

ILP:

This formulation creates a vertex cover and uses the fact that a maximum independent set consists of the complement of the vertices in a minimum vertex cover.

\begin{align*} \min \sum_{v \in V} x_v\\ \text{s.t.} &&\\ \forall (u, v) \in E: x_u + x_v \geq 1 && \text{(at least one vertex must be in a vertex cover of G)}\\ \end{align*}

graphilp.packing.max_indset.extract_solution(G, model)

Get a list of vertices comprising a maximum independent set

Parameters

• G – an ILPGraph

• model – a solved Gurobi model for maximum independent set

Returns

a list of vertices comprising a maximum independent set

graphilp.packing.clique_packing.create_model(G, clique_size)

Create an ILP for the clique packing problem

Parameters

• G – an ILPGraph

• clique_size – size of the clique to be packed

Returns

a gurobipy model

ILP:

Let \(k\) be the size of the cliques to be packed, \(\overline{E}\) be the complement of the edge set, and \(C = \{0, \ldots, \lfloor |V|/k \rfloor \}\) an index set for the possible cliques packed into \(G\).

The ILP formulation uses the following variables:

\(y_{c}\)	Binary variables indicating whether a clique with index \(c\) is used.
\(a_{cv}\)	Binary variables indicating whether vertex \(v\) is part of the clique with index \(c\).

\begin{align*} \max \sum_{c \in C} y_c\\ \text{s.t.} &&\\ \forall v \in V: \sum_{c \in C} a_{cv} \leq 1 && \text{(each vertex can be in at most one clique)}\\ \forall \{u, v\} \in \overline{E}: \forall c \in C:\\ a_{cu} + a_{cv} \leq 1 && \text{(unconnected vertices cannot be in the same clique)}\\ \forall c \in C: \sum_{v \in V} a_{cv} - k y_c = 0 && \text{(chosen cliques need to have k members)}\\ \forall c \in C: \forall v \in V: y_c - a_{cv} \geq 0 && \text{(cluster with } \geq 1 \text { vertex needs to be chosen as clique)}\\ \end{align*}

Example:

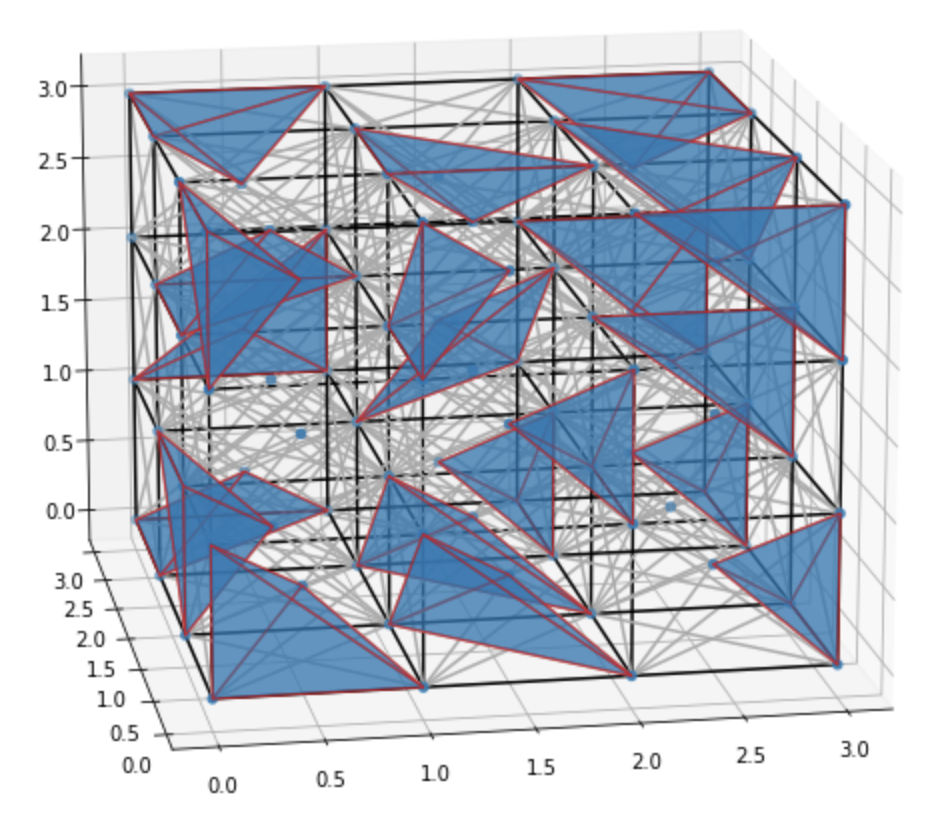
Packing tetrahedra How many vertex disjoint tetrahedra can you pack in a grid graph?

graphilp.packing.clique_packing.extract_solution(G, model)

Get a dictionary of vertex to clique assignments

If a vertex is not assigned to a clique, its value in the dictionary is zero.

Parameters

• G – an ILPGraph

• model – a solved Gurobi model for clique packing

Returns

a dictionary mapping vertices to cliques

graphilp.packing.set_packing.create_model(S, warmstart=[])

Create an ILP for the weighted set packing problem

Parameters

• S – a weighted ILPSetSystem

• warmstart – a list of disjoint sets in the set system

Returns

a gurobipy model

ILP:

Let \(M\) be the incidence matrix of the set system, \(w\) the vector of weights associated to the sets of the system, \(x\) a vector indicating which set is selected, and \(1\) a vector of ones.

\begin{align*} \max w^{\top}x\\ \text{s.t.} &&\\ Mx \leq 1 && \text{(each element of the universe is in at most one set)}\\ \end{align*}

graphilp.packing.set_packing.extract_solution(S, model)

Get a list of sets comprising a set packing

Parameters

• S – a weighted ILPSetSystem

• model – a solved Gurobi model for weighted set packing

Returns

a list of sets comprising a set packing

graphilp.packing.heuristics.setpacking_greedy.get_heuristic(S)

Greedy heuristic for the set packing problem

Iteratively add the set with highest size-to-weight ratio which does not contain an element that is already covered to the solution.

Parameters

S – a weighted ILPSetSystem

Returns

a list of disjoint sets of the set system