Covering

Covering problems in graphs are about finding substructures in a graph to which all other elements of the graph are adjacent. For example, in a vertex cover we look for a subset of the vertex set containing at least one end-point of each edge and hence covering all edges.

Dominating set

A dominating set in a graph \(G = (V, E)\) is a subset \(S \subset V\) of the vertex set such that each vertex \(v \in V\) is connected to a vertex \(s \in S\) by an edge \(\{s,v\} \in E\).

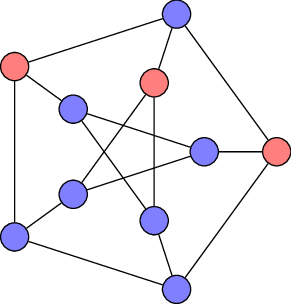
Figure made with TikZ

A minimum dominating set (red vertices) of the Petersen graph.

create_model

Create an ILP for the minimum dominating set problem

extract_solution

Get a list of edges comprising a dominating set

Edge dominating set

An edge dominating set in a graph \(G = (V, E)\) is a subset \(S \subseteq E\) of the edge set such that each edge in \(E\) is adjacent to an edge in \(S\).

_images/illustration_edge_dom.png

create_model

Create an ILP for the minimum edge dominating set problem

extract_solution

Get a list of edges comprising an edge dominating set

Vertex cover

A vertex cover in a graph \(G = (V, E)\) is a subset \(S \subset V\) of the vertex set such that for each edge \(\{u, v\} \in E\) at least one of its vertices is in \(S\): \(\{u,v\} \cap S \neq \emptyset\).

_images/illustration_covering.png

create_model

Create an ILP for the minimum vertex cover problem

extract_solution

Get a list of vertices comprising a vertex cover

Heuristics

The methods in this section provide approximate solutions to the vertex cover problem constituting admissible solutions from which to start the exact optimisation.

get_heuristic

Approximate solution to the minimum vertex cover problem via maximal matching heuristic

get_heuristic

Approximate solution to the minimum vertex cover problem via LP rounding

Knapsack

In the multi-dimensional knapsack problem the goal is to pack items with the highest total value into a knapsack where each item has a multi-dimensional weight vector and the knapsack has an individual capacity that cannot be exceeded in each dimension of the weight vector.

create_model

Create an ILP for the multi-dimensional knapsack problem

extract_solution

Get a list of items contained in the solution.

k-Cover

In the k-cover problem, the elements of the universe of a set system are to be covered by at most k sets of the system. The objective is then to maximise the total weight of the elements that are covered.

create_model

Greate an ILP for the k-cover problem

extract_solution

Get a list of sets comprising the k-cover

Set cover

The set cover problem is to find the smallest weight sub-collection of the sets in a set system such that all elements of the underlying universe are covered.

create_model

Greate an ILP for the set cover problem

extract_solution

Get a list of sets comprising a set cover

Heuristics

The methods in this section provide approximate solutions to the set cover problem constituting admissible solutions from which to start the exact optimisation.

get_heuristic

Greedy heuristic for the set cover problem

Details

graphilp.covering.min_dom_set.create_model(G)

Create an ILP for the minimum dominating set problem

Parameters

G – an ILPGraph

Returns

a gurobipy model

ILP:
\begin{align*} \min \sum_{v\in V}~x_v\\ \text{s.t.}&&\\ \forall v \in V:& \sum_{a\in \bigcup_{v\in e} e } x_a \geq 1 & \text{(each node is covered by a neighbour)} \end{align*}
Example:
_images/example_mindomset.png

Minimum dominating set

Find how many queens are needed to cover all squares on an \(n\times n\) chessboard.
graphilp.covering.min_dom_set.extract_solution(G, model)

Get a list of edges comprising a dominating set

Parameters

  • G – an ILPGraph

  • model – a solved Gurobi model for minimum dominating set

Returns

a list of nodes comprising a minimum dominating set

graphilp.covering.min_edge_dom.create_model(G)

Create an ILP for the minimum edge dominating set problem

Parameters

G – an ILPGraph

Returns

a gurobipy model

ILP:
\begin{align*} \min \sum_{e\in E}x_e\\ \text{s.t.}&&\\ \forall e \in E:& \sum_{a\in E ~:~e\cap a \neq \emptyset } x_a \geq 1 & \text{(each edge must be covered by an adjacent one)} \\ \end{align*}
graphilp.covering.min_edge_dom.extract_solution(G, model)

Get a list of edges comprising an edge dominating set

Parameters

  • G – an ILPGraph

  • model – a solved Gurobi model for minimum edge dominating set

Returns

a list of edges comprising a minimum edge dominating set

graphilp.covering.min_vertexcover.create_model(G, weight='weight', warmstart=[])

Create an ILP for the minimum vertex cover problem

Parameters

  • G – a weighted ILPGraph

  • weight – name of the weight parameter in the node dictionary of the graph

  • warmstart – a list of vertices forming a vertex cover of G

Returns

a gurobipy model

ILP:
\begin{align*} \min \sum_{v\in V} w_v x_v\\ \text{s.t.}&&\\ \forall \{k,j\} \in E: & x_k + x_j \geq 1 & \text{(at least one vertex in each edge is covered)} \end{align*}
graphilp.covering.min_vertexcover.extract_solution(G, model)

Get a list of vertices comprising a vertex cover

Parameters

  • G – an ILPGraph

  • model – a solved Gurobi model for minimum vertex cover

Returns

list of vertices of minimum vertex cover

graphilp.covering.heuristics.vertexcover_maximal_matching.get_heuristic(G)

Approximate solution to the minimum vertex cover problem via maximal matching heuristic

This heuristic successively chooses an edge in the graph, adds its vertices to the vertex cover and then deletes all edges adjacent to these vertices because they are already covered.

Parameters

G – an ILPGraph

Returns

a list of vertices forming a vertex cover of G

graphilp.covering.heuristics.vertexcover_lp_rounding.get_heuristic(G)

Approximate solution to the minimum vertex cover problem via LP rounding

Parameters

G – an ILPGraph

Returns

a list of vertices forming a vertex cover of G

LP:

The following LP with continuous node variables is rounded to obtain an approximation.

\begin{align*} \min \sum_{v\in V} x_v\\ \text{s.t.}&&\\ \forall \{u, v\} \in E: x_u + x_v \geq 1 && \text{(at least one vertex in each edge is covered)}\\ \forall v \in V: & x_v \geq 0\\ \forall v \in V: & x_v \leq 1\\ \end{align*}
graphilp.covering.knapsack.create_model(S, W)

Create an ILP for the multi-dimensional knapsack problem

Parameters

  • S – a weighted ILPSetSystem.

  • W – capacity of each knapsack

Returns

a gurobipy model

ILP:

Let \(M\) be the incidence matrix of the set system, \(w\) the vector of weights giving the value of the items to be packed and \(x\) a vector indicating which item is selected.

\begin{align*} \max w^{\top}x \\ \text{s.t.} &&\\ Mx \leq W && \text{(do not exceed capacity in any dimension)}\\ \end{align*}
graphilp.covering.knapsack.extract_solution(S, model)

Get a list of items contained in the solution.

Parameters

  • S – a weighted ILPSetSystem

  • model – a solved Gurobi model for the knapsack problem

Returns

list of items contained in the knapsack solution

graphilp.covering.k_cover.create_model(S, k, warmstart=[])

Greate an ILP for the k-cover problem

Parameters

  • S – a weighted ILPSetSystem

  • k – maximal number of sets in solution

  • warmstart – a list of sets forming a cover

Returns

a gurobipy model

ILP:

Let \(S\) be the collection of sets in the set system, \(U\) the underlying universe, and \(w_u\) the weight of each element \(u \in U\). For each \(s \in S\), the decision variable \(x_s\) indicates whether \(s\) is part of the solution. For each \(u \in U\), the decision variable \(y_u\) indicates whether \(u\) is covered in the solution.

\begin{align*} \max \sum_{u \in U} w_u y_u \\ \text{s.t.} &&\\ \forall u \in U: \sum_{s:u \in s}x_{s} \geq y_u && \text{(chosen sets cover elements of the universe)}\\ \sum_{s \in S} x_{s} \leq k && \text{(use at most k sets)}\\ \end{align*}
graphilp.covering.k_cover.extract_solution(S, model)

Get a list of sets comprising the k-cover

Parameters

  • S – a weighted ILPSetSystem

  • model – a solved Gurobi model for k coverage

Returns

list of sets contained in the solution of the k-cover

graphilp.covering.set_cover.create_model(S, warmstart=[])

Greate an ILP for the set cover problem

Parameters

  • S – a weighted ILPSetSystem

  • warmstart – a list of sets forming a cover

Returns

a gurobipy model

ILP:

Let \(S\) be the collection of sets in the set system, \(U\) the underlying universe, and \(w_s\) the weight of set \(s \in S\).

\begin{align*} \min \sum_{s \in S} w_{s} x_{s} \\ \text{s.t.} &&\\ \forall u \in U: \sum_{s:u \in s}x_{s} \geq 1 && \text{(cover every element of the universe)}\\ \forall s \in S: x_{s} \in \{0,1\} && \text{(every set is either in the set cover or not)}\\ \end{align*}
graphilp.covering.set_cover.extract_solution(S, model)

Get a list of sets comprising a set cover

Parameters

  • S – a weighted ILPSetSystem

  • model – a solved Gurobi model for weighted set cover

Returns

sets of the optimal set cover solution

graphilp.covering.heuristics.setcover_greedy.get_heuristic(S, k=None)

Greedy heuristic for the set cover problem

If paramter k is specified, the problem turns into a k-cover problem. In this case, the heuristic greedily approximates the maximal number of vertices that can be covered with at most k sets otherwise there is no limit on the number of sets.

Parameters

  • S – a weighted ILPSetSystem

  • k – maximal number of sets to use

Returns

a list of sets approximating the set cover problem