Matching

A matching in a graph \(G = (V, E)\) is a subset \(S \subseteq E\) of edges in which no pair of edges shares a vertex.

_images/illustration_matching.png

There are numerous natural optimisation questions on matchings, e.g., looking for perfect matchings (covering all vertices), maximal matchings (those that cannot be extended to a larger matching), maximum matchings (maximum cardinality), matching for certain classes of graphs, and matchings that optimise the weights of the edges involved in the matching.

An extensive discussion of matchings can be found in

General matching

create_model

Create an ILP for maximum weight matching

extract_solution

Get a list of the edges comprising the maximum weight matching

Perfect matching

A perfect matching in a graph is a matching in which each vertex of the graph is covered by an edge of the matching.

create_model

Create an ILP for maximum/minimum weight perfect matching

extract_solution

Get a list of the edges comprising the minimum/maximum weight perfect matching

Bipartite matching

For bipartite graphs, matching is usually much easier than for general graphs. The natural ILP for bipartite perfect matching is in fact a linear program: the integrality constraints are fulfilled automatically.

create_model

Create an ILP for maximum/minimum bipartite perfect matching

extract_solution

Get a list of the edges comprising the miniumum/maximum weight perfect bipartite matching

Details

graphilp.matching.maxweight.create_model(G, weight='weight')

Create an ILP for maximum weight matching

Parameters

  • G – a weighted ILPGraph

  • weight – name of the weight parameter in the edge dictionary of the graph

Returns

a gurobipy model

ILP:
\begin{align*} \max \sum_{\{i, j\} \in E} w_{ij} x_{ij}\\ \text{s.t.} &&\\ \forall \{u, v\} \in E: x_{uv} - x_u \leq 0 && \text{(choosing an edge implies choosing both of its vertices)}\\ \forall \{u, v\} \in E: x_{uv} - x_v \leq 0 && \text{(choosing an edge implies choosing both of its vertices)}\\ \forall v \in V: \sum_{\{u,v\} \in E} x_{uv} \leq 1 && \text{(at most one edge adjacent to each vertex)}\\ \end{align*}
graphilp.matching.maxweight.extract_solution(G, model)

Get a list of the edges comprising the maximum weight matching

Parameters

  • G – a weighted ILPGraph

  • model – a solved Gurobi model for maximum weight matching

Returns

a list of edges comprising the maximum weight matching

graphilp.matching.perfect.create_model(G, weight='weight', direction=- 1)

Create an ILP for maximum/minimum weight perfect matching

Parameters

  • G – a weighted ILPGraph

  • weight – name of the weight parameter in the edge dictionary of the graph

  • direction – GRB.MAXIMIZE for maximum weight matching, GRB.MINIMIZE for minimum weight matching

Returns

a gurobipy model

ILP:

Let \(n\) be the number of vertices in the graph.

\begin{align*} \max / \min \sum_{\{i, j\} \in E} w_{ij} x_{ij}\\ \text{s.t.} &&\\ \forall \{u, v\} \in E: x_{uv} = n/2&& \text{(} n/2 \text{ edges in matching)}\\ \forall v \in V: \sum_{\{u,v\} \in E} x_{uv} \leq 1 && \text{(at most one edge adjacent to each vertex)}\\ \end{align*}
graphilp.matching.perfect.extract_solution(G, model)

Get a list of the edges comprising the minimum/maximum weight perfect matching

Parameters

  • G – a weighted ILPGraph

  • model – a solved Gurobi model for maximum weight matching

Returns

a list of edges comprising the maximum weight matching

graphilp.matching.perfect_bipartite.create_model(G, A, weight='weight', direction=- 1)

Create an ILP for maximum/minimum bipartite perfect matching

Parameters

  • G – a weighted bipartite ILPGraph

  • A – subset of the vertex set of G giving the bipartition (each edge has exactly one end in A)

  • weight – name of the weight parameter in the edge dictionary of the graph

  • direction – GRB.MAXIMIZE for maximum weight matching, GRB.MINIMIZE for minimum weight matching

Returns

a gurobipy model

ILP:
\begin{align*} \max / \min \sum_{\{i, j\} \in E} w_{ij} x_{ij}\\ \text{s.t.} &&\\ \forall u \in A: \sum_{\{u,v\} \in E} x_{uv} = 1 && \text{(exactly one edge adjacent to each } u \in A\text{)}\\ \forall u \in V \setminus A: \sum_{\{u,v\} \in E} x_{uv} = 1 && \text{(exactly one edge adjacent to each } u \in V \setminus A\text{)}\\ \end{align*}

This is actually a linear program, i.e., solutions to the LP relaxation are automatically integral.

References:

Lovász, Plummer: Matching Theory, Chapter 7.1.

Example:
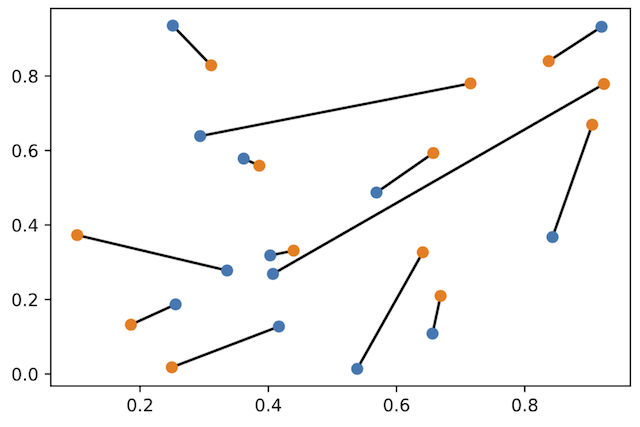
_images/example_bipartite.png

Two-coloured partitions

Learn how to use perfect matching in bipartite graphs to find a way

to connect n random blue points in the plane

to n random orange points without crossings.
graphilp.matching.perfect_bipartite.extract_solution(G, model)

Get a list of the edges comprising the miniumum/maximum weight perfect bipartite matching

Parameters

  • G – a weighted ILPGraph

  • model – a solved Gurobi model for minimum/maximum weight perfect bipartite matching

Returns

a list of edges comprising the minimum/maximum weight perfect bipartite matching