Networks¶

Graphs are very well-suited as models for networks. Typical questions in this area aim at the distribution of some commodity through a network. Such commodities could be water in a pipe network, bandwidth in a communications network, or goods in a supply chain.

Steiner Tree Problem¶

The Steiner Tree Problem in graphs asks for the shortest connection of a subset of the vertex set. This subset is usually called the set of terminals. While this problem is easy when all vertices are terminals (minimum spanning tree) or when there are only two terminals (shortest path), it is NP-hard otherwise. This means that unless P=NP, we expect any algorithm to become very slow for large instances. For this reason, we provide different formulations of the problem which may be more or less suitable for solving different types of instances.

Cycle-based constraint system¶

This formulation ensures that non-connected solutions must contain a cycle. Any cycles appearing in incumbent solutions are then avoided by explicitly adding constraints forbidding them through a callback.

`create_model`	Create an ILP for the minimum Steiner tree problem in graphs.
`extract_solution`	Get the optimal Steiner tree in G
`callback_cycle`	Callback inserts constraints to forbid cycles in solution candidates

Linear-size constraint system¶

Introducing vertex labels that increase along edges of the solution in the Steiner tree allows to give a formulation of linear size in the number of edges of the graph. Thus, the use of callback functions can be avoided.

`create_model`	Create an ILP for the minimum Steiner tree problem in graphs.
`extract_solution`	Get the optimal Steiner tree in G

There is also a version of this constraint system with somewhat stronger conditions on the labels:

`create_model`	Create an ILP for the minimum Steiner tree problem in graphs.
`extract_solution`	Get the optimal Steiner tree in G

Heuristics¶

Approximate solutions can be used as a warmstart in the optimisation, usually leading to shorter running times. Constant factor approximations also imply a lower bound on the solution.

get_heuristic

Approximation to the Steiner tree problem by metric closure

Prize Collecting Steiner Tree (PCST)¶

The Prize Collecting Steiner Tree Problem is similar to the Steiner Tree Problem in that a lowest weight network spanning a given set of vertices is desired. However, each vertex comes with a prize value that is counted against the edge weights and it is a part of the problem to select a subset of the vertex set that optimises the total prize against the total cost of the network.

Cycle-based constraint system¶

This formulation ensures that non-connected solutions must contain a cycle. Any cycles appearing in incumbent solutions are then avoided by explicitly adding constraints forbidding them through a callback.

`create_model`	Create an ILP for the Prize Collecting Steiner Tree Problem.
`extract_solution`	Get the optimal prize collecting Steiner tree in G
`callback_cycle`	Callback inserts constraints to forbid cycles in solution candidates

Linear-size constraint system¶

Introducing vertex labels that increase along edges of the solution in the prize collecting Steiner tree allows to give a formulation of linear size in the number of edges of the graph. Thus, the use of callback functions can be avoided.

`create_model`	Create an ILP for the Prize Collecting Steiner Tree Problem.
`extract_solution`	Get the optimal prize collecting Steiner tree in G

Travelling Salesman Problem (TSP)¶

The Travelling Salesman Problem is one of the most well-known problems of combinatorial optimisation. Given a list of cities (nodes in a graph) and distances between all pairs of cities (weighted edges in a graph), a solution to this problem is a shortest tour going through all cities but visiting no city twice.

Depending on whether the tour needs to start where it began and on the properties of the distances (for example they can be required to give a metric) there are many variants of the problem.

Asymmetric TSP¶

In the asymmetric case, the underlying graph is directed and the distance from A to B may be different from the distance from B to A.

Generic¶

Introducing vertex labels that increase along the edges of the tour allows to give a formulation of linear size in the number of edges of the graph. Thus, the use of callback functions can be avoided.

`create_model`	Create an ILP for the min/max path asymmetric TSP
`extract_solution`	Get the optimal tour in G

This formulation ensures that solutions are a disjoint union of cycles. More than one cycle appearing in incumbent solutions is then avoided by explicitly adding constraints forbidding this through a callback (sub-tour elimination).

`create_model`	Create an ILP for the min/max path asymmetric TSP
`extract_solution`	Get the optimal tour in G

ATSP¶

`create_model`	Create an ILP for the min/max asymmetric TSP
`extract_solution`	Get the optimal tour in G

`create_model`	Faster formulation for the min/max asymmetric TSP
`extract_solution`	Get the optimal tour in G

Path ATSP¶

In the path version, the tour may start and end in different vertices.

`create_model`	Create an ILP for the min/max asymmetric path TSP
`extract_solution`	Get the optimal tour in G

Metric TSP¶

In the metric TSP, the edge weights form a metric on the graph, i.e., they obey the triangle inequality \(w_{uv} \leq w_{ux} + w_{xv}\) for any three vertices \(u, v, x\).

`create_model`	Create an ILP for the min/max metric TSP
`extract_solution`	Get the optimal tour in G

Path TSP¶

In the path version, the tour may start and end in different vertices.

`create_model`	Create an ILP for the min/max metric path TSP
`extract_solution`	Get the optimal tour in G

Heuristics¶

Approximate solutions can be used as a warmstart in the optimisation, usually leading to shorter running times. Constant factor approximations also imply a lower bound on the solution.

get_heuristic

Approximation to TSP by Christofides’s algorithm

get_heuristic

Nearest neighbour heuristic for TSP

get_heuristic

2 Opt - Improvement heuristic for the Traveling Salesman Problem

Details¶

graphilp.network.steiner.callback_cycle(model, where)¶

Callback inserts constraints to forbid cycles in solution candidates

Parameters

model – a gurobipy model
where – a Gurobi callback parameter indicating from which step of the optimisation the callback originated

graphilp.network.steiner.create_model(G, terminals, weight='weight', warmstart=[], lower_bound=None)¶

Create an ILP for the minimum Steiner tree problem in graphs.

This formulation enforces a cycle in the solution if it is not connected. A callback will detect cycles and add constraints to explicity forbid them. Together, this ensures that the solution is a tree.

Parameters

G – a weighted ILPGraph
terminals – a list of vertices that need to be connected by the Steiner tree
weight – name of the argument in the edge dictionary of the graph used to store edge cost
warmstart – a list of edges forming a tree in G connecting all terminals
lower_bound – give a known lower bound to the solution length

Returns

a gurobipy model

Callbacks:

This model uses callbacks which need to be included when calling Gurobi’s optimize function:

model.optimize(callback = callback_cycle)

ILP:

Let \(T\) be the set of terminals.

\begin{align*} \min \sum_{(u,v) \in E} w_{uv} x_{uv}\\ \text{s.t.} &&\\ \forall t \in T: x_t = 1 && \text{(require terminals to be chosen)}\\ \sum_{v\in V} x_v - \sum_{\{u,v\}\in E} x_{uv} = 1 && \text{(enforce cycle when graph is not connected)}\\ \forall \{u,v\}\in E: 2x_{uv} - x_u - x_v \leq 0 && \text{(require vertices to be chosen when edge is chosen)}\\ \forall i \in V: x_i-\sum_{u=i \vee v=i}x_{uv} \leq 0 && \text{(forbid isolated vertices)}\\ \end{align*}

The callbacks add a new constraint for each cycle \(C\) of length \(\ell(C)\) coming up in a solution candidate:

\begin{align*} \sum_{\{u, v\} \in C} x_{uv} < \ell(C) && \text{(forbid including complete cycle)} \end{align*}

Example:

Steiner trees

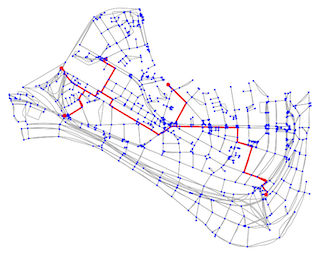
Find the shortest tree connecting a given set of nodes in a graph.

graphilp.network.steiner.extract_solution(G, model)¶

Get the optimal Steiner tree in G

Parameters

G – a weighted ILPGraph
model – a solved Gurobi model for the minimum Steiner tree problem

Returns

the edges of an optimal Steiner tree connecting all terminals in G

graphilp.network.steiner_linear.create_model(G, terminals, weight='weight', warmstart=[], lower_bound=None)¶

Create an ILP for the minimum Steiner tree problem in graphs.

This formulation enforces a cycle in the solution if it is not connected. Cycles are then forbidden by enforcing an increasing labelling along the edges of the solution. To this end, the formulation is working with a directed graph internally.

Parameters

G – a weighted ILPGraph
terminals – a list of vertices that need to be connected by the Steiner tree
weight – name of the argument in the edge dictionary of the graph used to store edge cost
warmstart – a list of edges forming a tree in G connecting all terminals
lower_bound – give a known lower bound to the solution length

Returns

a gurobipy model

ILP:

Let \(n = |V|\) be the number of vertices in \(G\) and \(T\) the set of terminals. Further, let \(\overrightarrow{E} := \{(u, v), (v, u) \mid \{u, v\} \in E\}\) be the directed edge set used in the internal representation.

\begin{align*} \min \sum_{(u,v) \in \overrightarrow{E}} w_{uv} x_{uv}\\ \text{s.t.} &&\\ \forall \{u,v\} \in E: x_{uv} + x_{vu} \leq 1 && \text{(restrict edges to one direction)}\\ \forall t \in T: x_t = 1 && \text{(require terminals to be chosen)}\\ \sum_{v \in V} x_v - \sum_{(u, v) \in \overrightarrow{E}} x_{uv} = 1 && \text{(enforce cycle when graph}\\ && \text{is not connected)}\\ \forall \{u,v\}\in E: 2(x_{uv}+x_{vu}) - x_u - x_v \leq 0 && \text{(require vertices to be chosen}\\ && \text{when edge is chosen)}\\ \forall i \in V: x_i-\sum_{u=i \vee v=i}x_{uv} \leq 0 && \text{(forbid isolated vertices)}\\ \forall \{u,v\}\in E: n x_{uv} + \ell_v - \ell_u \geq 1 - n(1-x_{vu}) && \text{(enforce increasing labels)}\\ \forall \{u,v\}\in E: n x_{vu} + \ell_u - \ell_v \geq 1 - n(1-x_{uv}) && \text{(enforce increasing labels)}\\ \forall v \in V: \sum_{(u,v) \in \overrightarrow{E}} x_{uv} \leq 1 && \text{(only one arrow into each vertex)}\\ \end{align*}

Example:

Steiner trees

Find the shortest tree connecting a given set of nodes in a graph.

graphilp.network.steiner_linear.extract_solution(G, model)¶

Get the optimal Steiner tree in G

Parameters

G – a weighted ILPGraph
model – a solved Gurobi model for the minimum Steiner tree problem

Returns

the edges of an optimal Steiner tree connecting all terminals in G

graphilp.network.steiner_linear_tightened.create_model(G, terminals, root=None, weight='weight', warmstart=[], lower_bound=None)¶

Create an ILP for the minimum Steiner tree problem in graphs.

This formulation enforces a cycle in the solution if it is not connected. Cycles are then forbidden by enforcing an increasing labelling along the edges of the solution. To this end, the formulation is working with a directed graph internally. As a slight modification of graphilp.network.steiner_linear, the constraints enforce that the labels increase by one along each edge in the solution.

Parameters

G – a weighted ILPGraph
terminals – a list of nodes that need to be connected by the Steiner tree
root – a terminal chosen as the root of the Steiner tree
weight – name of the argument in the edge dictionary of the graph used to store edge cost
warmstart – a list of edges forming a tree in G connecting all terminals
lower_bound – give a known lower bound to the solution length

Returns

a gurobipy model

ILP:

Let \(n = |V|\) be the number of vertices in \(G\), \(T\) the set of terminals, and \(r\) be a terminal chosen as the root of the Steiner tree. Further, let \(\overrightarrow{E} := \{(u, v), (v, u) \mid \{u, v\} \in E\}\) be the directed edge set used in the internal representation.

\begin{align*} \min \sum_{(u,v) \in \overrightarrow{E}} w_{uv} x_{uv}\\ \text{s.t.} &&\\ \forall \{u,v\} \in E: x_{uv} + x_{vu} \leq 1 && \text{(restrict edges to one direction)}\\ \ell_r = 1 && \text{(root label is set to 1)}\\ \forall t \in T: x_t = 1 && \text{(require terminals to be chosen)}\\ \sum_{v \in V} x_v - \sum_{(u, v) \in \overrightarrow{E}} x_{ij} = 1 && \text{(enforce circle when graph}\\ && \text{is not connected)}\\ \forall \{u,v\}\in E: 2(x_{uv}+x_{vu}) - x_u - x_v \leq 0 && \text{(require vertices to be chosen}\\ && \text{when edge is chosen)}\\ \forall i \in V: x_i-\sum_{u=i \vee v=i}x_{uv} \leq 0 && \text{(forbid isolated nodes)}\\ \forall \{u,v\}\in E: \ell_v - 2nx_{vu} \leq \ell_u + 1 + 2n(1-x_{uv}) && \text{(enforce increasing labels)}\\ \forall \{u,v\}\in E: \ell_u + 1 \leq 2nx_{vu} + \ell_v + 2n(1-x_{uv}) && \text{(enforce increasing labels)}\\ \forall \{u,v\}\in E: \ell_u - 2nx_{uv} \leq \ell_v + 1 + 2n(1-x_{vu}) && \text{(enforce increasing labels)}\\ \forall \{u,v\}\in E: \ell_v + 1 \leq 2nx_{uv} + \ell_u + 2n(1-x_{vu}) && \text{(enforce increasing labels)}\\ \forall v \in V: \ell_v - n x_v \leq 1&& \text{(set label to 1 when}\\ && \text{vertex is not chosen)}\\ \forall v \in V: \sum_{(u,v) \in \overrightarrow{E}} x_{uv} \leq 1 && \text{(only one arrow into each vertex)}\\ \end{align*}

Example:

Steiner trees

Find the shortest tree connecting a given set of nodes in a graph.

graphilp.network.steiner_linear_tightened.extract_solution(G, model)¶

Get the optimal Steiner tree in G

Parameters

G – a weighted ILPGraph
model – a solved Gurobi model for the minimum Steiner tree problem

Returns

the edges of an optimal Steiner tree connecting all terminals in G

graphilp.network.heuristics.steiner_metric_closure.get_heuristic(G, terminals, weight='weight')¶

Approximation to the Steiner tree problem by metric closure

Creates a minimum weight spanning tree in the metric closure of terminals in the graph. This is a 2-approximation to the Steiner tree problem and hence also gives a lower bound.

Parameters

G – a weighted ILPGraph
terminals – a list of vertices that need to be connected by the Steiner tree
weight – name of the argument in the edge dictionary of the graph used to store edge cost

Returns

a list of edges forming the approximate solution and a lower bound on the optimal solution

Example:

warmstart, lower_bound = steiner_metric_closure.getHeuristic(G, terminals)

m = create_model(G, terminals, weight='length', warmstart=warmstart, lower_bound=lower_bound)

graphilp.network.pcst.callback_cycle(model, where)¶

Callback inserts constraints to forbid cycles in solution candidates

Parameters

model –
a gurobipy model
where – a Gurobi callback parameter indicating from which step of the optimisation the callback originated

graphilp.network.pcst.create_model(G, forced_terminals=[], weight='weight', prize='prize', warmstart=[], lower_bound=None)¶

Create an ILP for the Prize Collecting Steiner Tree Problem.

This formulation enforces a cycle in the solution if it is not connected. A callback will detect cycles and add constraints to explicity forbid them. Together, this ensures that the solution is a tree.

Parameters

G – a weighted ILPGraph
forced_terminals – list of terminals that have to be connected
weight – name of the argument in the edge dictionary of the graph used to store edge cost
prize – name of the argument in the vertex dictionary of the graph used to store vertex prize values
warmstart – a list of edges forming a tree in G connecting all terminals
lower_bound – give a known lower bound to the solution length

Returns

a gurobipy model

Callbacks:

This model uses callbacks which need to be included when calling Gurobi’s optimize function:

model.optimize(callback = callback_cycle)

ILP:

Let \(T_f\) be the set of forced terminals required to be part of the solution. Further, let \(p_v\) be the prize associated with each vertex \(v\).

\begin{align*} \max \sum_{v \in V} p_v x_v- \sum_{\{u,v\} \in E} w_{uv} x_{uv}\\ \text{s.t.} &&\\ \forall \{u,v\}\in E: x_{uv} + x_{vu} \leq 1 && \text{(restrict edges to one direction)}\\ \forall t \in T_f: x_t = 1 && \text{(require forced terminals to be chosen)}\\ \sum_{v\in V} x_v - \sum_{\{u,v\}\in E} x_{uv} = 1 && \text{(enforce circle when graph is not connected)}\\ \forall \{u,v\}\in E: 2x_{uv} - x_u - x_v \leq 0 && \text{(require vertices to be chosen when edge is chosen)}\\ \forall i \in V: x_i-\sum_{u=i \vee v=i}x_{uv} \leq 0 && \text{(forbid isolated vertices)}\\ \end{align*}

The callbacks add a new constraint for each cycle \(C\) of length \(\ell(C)\) coming up in a solution candidate:

\begin{align*} \sum_{\{u, v\} \in C} x_{uv} < \ell(C) && \text{(forbid including complete cycle)} \end{align*}

graphilp.network.pcst.extract_solution(G, model)¶

Get the optimal prize collecting Steiner tree in G

Parameters

G – an ILPGraph
model – a solved Gurobi model for Prize Collecting Steiner tree

Returns

the edges of an optimal prize collecting Steiner tree

graphilp.network.pcst_linear.create_model(G, forced_terminals=[], weight='weight', prize='prize', warmstart=[], lower_bound=None)¶

Create an ILP for the Prize Collecting Steiner Tree Problem.

This formulation enforces a cycle in the solution if it is not connected. Cycles are then forbidden by enforcing an increasing labelling along the edges of the solution. To this end, the formulation is working with a directed graph internally.

Parameters

G – a weighted ILPGraph
forced_terminals – list of terminals that have to be connected
weight – name of the argument in the edge dictionary of the graph used to store edge cost
prize – name of the argument in the vertex dictionary of the graph used to store vertex prize values
warmstart – a list of edges forming a tree in G connecting all terminals
lower_bound – give a known lower bound to the solution length

Returns

a gurobipy model

ILP:: Let \(n\) be the number of vertices in the graph and \(T_f\) be the set of forced terminals required to be part of the solution. Further, let \(p_v\) be the prize associated with each vertex \(v\) and \(\overrightarrow{E} := \{(u, v), (v, u) \mid \{u, v\} \in E\}\) be the directed edge set used in the internal representation.

\begin{align*} \max \sum_{v \in V} p_v x_v- \sum_{(u,v) \in E} w_{uv} x_{uv}\\ \text{s.t.} &&\\ \forall \{u,v\}\in E: x_{uv} + x_{vu} \leq 1 && \text{(restrict edges to one direction)}\\ \forall t \in T_f: x_t = 1 && \text{(require forced terminals}\\ && \text{to be chosen)}\\ \sum_{v\in V} x_v - \sum_{(u,v) \in \overrightarrow{E}} x_{uv} = 1 && \text{(enforce circle when graph}\\ && \text{is not connected)}\\ \forall \{u,v\}\in E: 2(x_{uv}+x_{vu}) - x_u - x_v \leq 0 && \text{(require vertices to be chosen}\\ && \text{when edge is chosen)}\\ \forall i \in V: x_i-\sum_{u=i \vee v=i}x_{uv} \leq 0 && \text{(forbid isolated vertices)}\\ \forall \{u,v\}\in E: n x_{uv} + \ell_v - \ell_u \geq 1 - n(1-x_{vu}) && \text{(enforce increasing labels)}\\ \forall \{u,v\}\in E: n x_{vu} + \ell_u - \ell_v \geq 1 - n(1-x_{uv}) && \text{(enforce increasing labels)}\\ \forall v \in V: \sum_{(u,v) \in \overrightarrow{E}} x_{uv} \leq 1 && \text{(only one arrow into each vertex)}\\ \end{align*}

graphilp.network.pcst_linear.extract_solution(G, model)¶

Get the optimal prize collecting Steiner tree in G

Parameters

G – a weighted ILPGraph
model – a solved Gurobi model for Prize Collecting Steiner tree

Returns

the edges of an optimal prize collecting Steiner tree

graphilp.network.atsp.create_model(G, direction=- 1, weight='weight', warmstart=[])¶

Create an ILP for the min/max asymmetric TSP

Uses graphilp.network.gen_path_atsp.create_model() to set up the problem.

Parameters

G – a weighted ILPGraph
direction – GRB.MAXIMIZE for maximum weight tour, GRB.MINIMIZE for minimum weight tour
weight – name of the weight parameter in the edge dictionary of the graph
warmstart – a list of edges forming a tour

Returns

a gurobipy model

graphilp.network.atsp.extract_solution(G, model)¶

Get the optimal tour in G

Parameters

G – a weighted ILPGraph
model – a solved Gurobi model for min/max asymmetric TSP

Returns

the edges of an optimal tour in G

graphilp.network.atsp_desrochers_laporte.create_model(G, direction=- 1, metric='', weight='weight', warmstart=[])¶

Faster formulation for the min/max asymmetric TSP

This formulation implements a formulation from Desrochers and Laporte (1990): Improvements and extensions to the Miller–Tucker–Zemlin subtour elimination constraints

Parameters

G – a complete weighted ILPGraph
direction – GRB.MAXIMIZE for maximum weight tour, GRB.MINIMIZE for minimum weight tour
metric – ‘metric’ for symmetric problem otherwise asymmetric problem
weight – name of the weight parameter in the edge dictionary of the graph
warmstart – a list of edges forming a tour

Returns

a gurobipy model

ILP:: Let \(s\) be an arbitrary starting node for the tour.

\begin{align*} \min / \max \sum_{(u,v) \in E} w_{uv} x_{uv}\\ \text{s.t.} &&\\ \forall v \in V: \sum_{(u, v) \in E}x_{uv} = 1 && \text{(exactly one incoming edge)}\\ \forall u \in V: \sum_{(u, v) \in E}x_{uv} = 1 && \text{(exactly one outgoing edge)}\\ \forall u, v \in V \setminus \{s\}: \\ \ell_u - \ell_v + (n-1)x_{uv} + (n-3)x_{vu} \leq n-2 && \text{(labels increase by one in edge direction)}\\ \\ \forall u \in V \setminus \{s\}:\\ -\ell_u + (n-3)x_{us} + \sum_{v \in V \setminus \{s\}}x_{vu} \leq -1 && \text{(subtour elimination)}\\ \\ \forall u \in V \setminus \{s\}:\\ \ell_u + (n-3)x_{su} + \sum_{v \in V \setminus \{s\}}x_{uv} \leq n-1 && \text{(subtour elimination)}\\ \end{align*}
References:: See Roberti and Toth: Models and algorithms for the Asymmetric Traveling Salesman Problem: an experimental comparison for this formulation in context.

graphilp.network.atsp_desrochers_laporte.extract_solution(G, model)¶

Get the optimal tour in G

Parameters

G – a complete weighted ILPGraph
model – a solved Gurobi model for min/max asymmetric TSP

Returns

the edges of an optimal tour in G

graphilp.network.gen_path_atsp.create_model(G, direction=- 1, metric='', weight='weight', start=None, end=None, warmstart=[])¶

Create an ILP for the min/max path asymmetric TSP

Parameters

G – a weighted ILPGraph
direction – GRB.MAXIMIZE for maximum weight tour, GRB.MINIMIZE for minimum weight tour
metric – ‘metric’ for symmetric problem otherwise asymmetric problem
weight – name of the weight parameter in the edge dictionary of the graph
start – require the TSP path to start at this vertex
end – require the TSP path to end at this vertex
warmstart – a list of edges forming a tour

Returns

a gurobipy model

ILP:: Let \(s\) be the start vertex (if it is specified), \(e\) the end vertex, and \(n\) the number of vertices. If no start vertex is given, let \(s\) be any fixed vertex.

\begin{align*} \min / \max \sum_{(u,v) \in E} w_{uv} x_{uv}\\ \text{s.t.} &&\\ \forall v \in V \setminus \{s, e\}: \sum_{(u, v) \in E}x_{uv} = 1 && \text{(exactly one incoming edge)}\\ \forall v \in V \setminus \{s, e\}: \sum_{(v, u) \in E}x_{vu} = 1 && \text{(exactly one outgoing edge)}\\ \sum_{(s, v) \in E}x_{sv} = 1 && \text{(exactly one outgoing edge from start vertex)}\\ \sum_{(v, e) \in E}x_{ve} = 1 && \text{(exactly one incoming edge to end vertex)}\\ \sum_{(v, s) \in E}x_{vs} = 0 && \text{(no incoming edge to start vertex)}\\ \sum_{(e, v) \in E}x_{ev} = 0 && \text{(no outgoing edge from end vertex)}\\ \ell_s = 0 && \text{(start vertex has label 0)}\\ \ell_e = n-1 && \text{(end vertex has label } n-1 \text{)}\\ \forall (u,v) \in E \setminus \{(u, s)\mid u \in V \}:\\ \ell_u - \ell_v + nx_{uv} \leq n-1 && \text{(increasing labels along tour)}\\ \end{align*}

graphilp.network.gen_path_atsp.extract_solution(G, model)¶

Get the optimal tour in G

Parameters

G – a weighted ILPGraph
model – a solved Gurobi model for min/max path asymmetric TSP

Returns

the edges of an optimal tour/path in G

graphilp.network.path_atsp.create_model(G, start, end, direction=- 1, weight='weight', warmstart=[])¶

Create an ILP for the min/max asymmetric path TSP

Uses graphilp.network.gen_path_atsp.create_model() to set up the problem.

Parameters

G – a weighted ILPGraph
start – a vertex of the graph G in which the ATSP path should start
end – a vertex of the graph G in which the ATSP path should end
direction – GRB.MAXIMIZE for maximum weight tour, GRB.MINIMIZE for minimum weight tour
weight – name of the weight parameter in the edge dictionary of the graph
warmstart – a list of edges forming a tour

Returns

a gurobipy model

graphilp.network.path_atsp.extract_solution(G, model)¶

Get the optimal tour in G

Parameters

G – a weighted ILPGraph
model – a solved Gurobi model for min/max asymmetric path TSP

Returns

the edges of an optimal tour in G

graphilp.network.path_tsp.create_model(G, start, end, direction=- 1, weight='weight', warmstart=[])¶

Create an ILP for the min/max metric path TSP

Uses graphilp.network.gen_path_atsp.create_model() to set up the problem.

Parameters

G – a weighted ILPGraph
start – a vertex of the graph G in which the TSP path should start
end – a vertex of the graph G in which the TSP path should end
direction – GRB.MAXIMIZE for maximum weight tour, GRB.MINIMIZE for minimum weight tour
weight – name of the weight parameter in the edge dictionary of the graph
warmstart – a list of edges forming a tour

Returns

a gurobipy model

graphilp.network.path_tsp.extract_solution(G, model)¶

Get the optimal tour in G

Parameters

G – a weighted ILPGraph
model – a solved Gurobi model for min/max metric path TSP

Returns

the edges of an optimal tour in G

graphilp.network.tsp.create_model(G, direction=- 1, weight='weight', warmstart=[])¶

Create an ILP for the min/max metric TSP

Uses graphilp.network.gen_path_atsp.create_model() to set up the problem.

Parameters

G – a weighted ILPGraph
direction – GRB.MAXIMIZE for maximum weight tour, GRB.MINIMIZE for minimum weight tour
weight – name of the weight parameter in the edge dictionary of the graph
warmstart – a list of edges forming a tour

Returns

a gurobipy model

Example:

TSP art

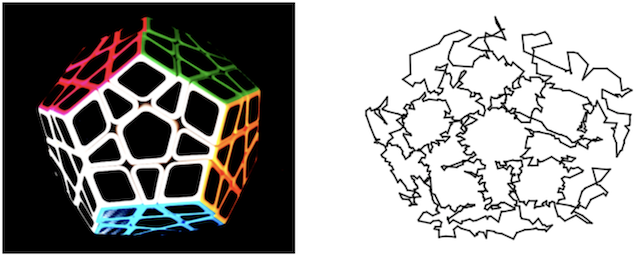
Transform an image into line art that can be drawn without lifting the pencil.

graphilp.network.tsp.extract_solution(G, model)¶

Get the optimal tour in G

Parameters

G – a weighted ILPGraph
model – a solved Gurobi model for min/max metric TSP

Returns

the edges of an optimal tour in G

graphilp.network.tsp_callbacks.callback_cycle(model, where)¶

Callback inserts constraints to forbid more than one cycle in solution candidates

Parameters

model –
a gurobipy model
where – a Gurobi callback parameter indicating from which step of the optimisation the callback originated

graphilp.network.tsp_callbacks.create_model(G, direction=- 1, metric='', weight='weight', start=None, end=None, warmstart=[])¶

Create an ILP for the min/max path asymmetric TSP

This formulation enforces that the solution has at least one cycle. A callback will detect if there is more than one cycle and adds constraints to explicity forbid this. Together, this ensures that the solution is a valid tour.

Parameters

G – a weighted ILPGraph
direction – GRB.MAXIMIZE for maximum weight tour, GRB.MINIMIZE for minimum weight tour
metric – ‘metric’ for symmetric problem otherwise asymmetric problem
weight – name of the weight parameter in the edge dictionary of the graph
start – require the TSP path to start at this vertex
end – require the TSP path to end at this vertex
warmstart – a list of edges forming a tour

Returns

a gurobipy model

Callbacks:

This model uses callbacks which need to be included when calling Gurobi’s optimize function:

model.optimize(callback = callbackCycle)

ILP:

Let \(s\) be the start node (if it is specified) and \(e\) the end node.

\begin{align*} \min / \max \sum_{(i,j) \in E} w_{ij} x_{ij}\\ \text{s.t.} &&\\ \forall v \in V \setminus \{s, e\}: \sum_{(u, v) \in R}x_{uv} = 1 && \text{(Exactly one outgoing edge.)}\\ \forall v \in V \setminus \{s, e\}: \sum_{(v, u) \in R}x_{vu} = 1 && \text{(Exactly one incoming edge.)}\\ \sum_{(s, v) \in R}x_{sv} = 1 && \text{(Exactly one outgoing edge from start node.)}\\ \sum_{(v, e) \in R}x_{ve} = 1 && \text{(Exactly one incoming edge to end node.)}\\ \end{align*}

graphilp.network.tsp_callbacks.extract_solution(G, model)¶

Get the optimal tour in G

Parameters

G – a weighted ILPGraph
model – a solved Gurobi model for min/max path asymmetric TSP

Returns

the edges of an optimal tour/path in G

graphilp.network.heuristics.tsp_christofides.get_heuristic(G, weight='weight')¶

Approximation to TSP by Christofides’s algorithm

Creates a TSP tour from a minimum weight spanning tree by applying a minimum weight perfect matching to the nodes of odd degree in the spanning tree. This gives a low-weight Eulerian subgraph. An Euler tour in it can be used to create a TSP tour by skipping over vertices that are visited more than once.

This is a 3/2-approximation to the metric TSP and hence also gives a lower bound.

Parameters

G – a weighted ILPGraph
weight – name of the argument in the edge dictionary of the graph used to store edge cost

Returns

a list of edges forming the approximate solution and a lower bound on the optimal solution

Example:

warmstart, lower_bound = tsp_christofides.get_heuristic(G)

m = create_model(G, warmstart=warmstart, lower_bound=lower_bound)

graphilp.network.heuristics.tsp_nearest_neighbour.get_heuristic(G, weight='weight')¶

Nearest neighbour heuristic for TSP

Create a tour by greedily moving to the nearest neighbour that has not yet been visited in each step.

Parameters

G – a weighted ILPGraph
weight – name of the argument in the edge dictionary of the graph used to store edge cost

Returns

a list of edges forming the approximate solution and its length

graphilp.network.heuristics.tsp_two_opt.find_tour_length(tour, G)¶: Compute the length of a given tour

graphilp.network.heuristics.tsp_two_opt.get_heuristic(G, tour, length)¶

2 Opt - Improvement heuristic for the Traveling Salesman Problem

Improve a tour, e.g., one returned from the Nearest Neighbour Heuristic. Do this by exchanging the role of two vertices \(i\) and \(j\) iteratively as follows if it leads to a shorter tour:

Replace the tour

\(s \xrightarrow{p_{su}} u \rightarrow i \xrightarrow{p_{ij}} j \rightarrow v \xrightarrow{p_{ve}} e\)

by

\(s \xrightarrow{p_{su}} u \rightarrow j \xrightarrow{p_{ji}} i \rightarrow v \xrightarrow{p_{ve}} e\)

Parameters

G – a weighted ILPGraph
tour – a list of edges describing a tour
length – length of the tour

Returns

a list of edges forming the approximate solution and its length

graphilp.network.heuristics.tsp_two_opt.iterate_inner(G, tour, length, cities, i)¶: Try all ending points \(j\) in the tour for swapping.

graphilp.network.heuristics.tsp_two_opt.iterate_outer(G, tour, length, cities)¶: Try all starting points \(i\) in the tour for swapping.

graphilp.network.heuristics.tsp_two_opt.two_opt_swap(i, j, tour)¶

Swap two cities in the tour

Replace the tour

\(s \xrightarrow{p_{su}} u \rightarrow i \xrightarrow{p_{ij}} j \rightarrow v \xrightarrow{p_{ve}} e\)

by

\(s \xrightarrow{p_{su}} u \rightarrow j \xrightarrow{p_{ji}} i \rightarrow v \xrightarrow{p_{ve}} e\)